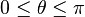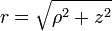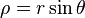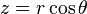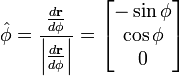구면 좌표계(spherical coordinate system) 직교 좌표계(rectangular coordinate system)

Computer Graphics

구면 좌표계(spherical coordinate system) 직교 좌표계(rectangular coordinate system)

익플루 2014. 2. 24. 21:06

3D에서 꼭 알아야할

구면좌표계 직교좌표계

1. 구면 좌표계

구면좌표계 (球面座標係, spherical coordinate system)는 3차원 공간 상의 점들을 나타내는 좌표계의 하나로, 보통 $(r,\theta ,\phi )$ 로 나타낸다.

원점에서의 거리 $r$ 은 0부터 $\color {Blue}\infty$ 까지,

양의 방향의 z축과 이루는 각도 $\theta$ 는 0부터 $\pi$ 까지,

z축을 축으로 양의 방향의 x축과 이루는 각 $\phi$ 는 0부터 $2\pi$ 까지의 값을 갖는다.

$\theta$ 는 위도로, $\phi$ 는 경도로 표현되는 경우도 있다.

이 세 수치를 보고, 다음과 같은 방법으로 공간의 점을 찾을 수 있다.:

원점 $(0,0,0)$ 에서 $r$ 만큼 z축을 따라 간다.

그 지점에서 xz 평면 안에 있으면서 z축에서부터 $\theta$ 만큼 회전한다.

이 xz 평면 전체를 z축을 축으로 $\phi$ 만큼 반 시계방향(+x축에서 +y축 방향으로)으로 돌린다.

구면좌표계라는 이름은 이 좌표계에서 ' $r=1$ '이 단위구(單位球)를 표현하기 때문에 붙여졌다.

구면좌표계와 원통좌표계는 평면 극좌표계를 공간으로 확장한 것이며, 구면좌표계는 구대칭이 나타나는 문제에서 유용하게 쓰인다.

예를 들어, 수소원자와 같이 구대칭이 있는 경우에 슈뢰딩거 방정식을 풀 때 구면좌표계를 사용한다.

아래 변환식을 통해 직교좌표계와 변환할 수 있지만, 변환식에서 사용하는 역삼각함수는 일의적이지 않기 때문에, 공간상의 각 점마다 하나의 좌표만 대응하는 직교좌표계와는 달리, 구면좌표계는 한 점을 나타내는 표현이 여러가지일 수 있다. 예를 들어, (1, 0°, 0°), (1, 0°, 45°), 과 (-1, 180°, 270°) 는 모두 같은 점을 나타낸다.

Spherical coordinate.gif

좌표 $(r,\theta ,\phi )$ 는 다음과 같이 정의 된다. 주어진 점을 P라 하자.

$\color {Blue}r$ : 원점으로부터 P까지의 거리.
$\color {Blue}\theta$ : z축의 양의 방향으로부터 원점과 P가 이루는 직선까지의 각
$\color {Blue}\phi$ : x축의 양의 방향으로부터 원점과 P가 이루는 직선을 xy평면에 투영시킨 직선까지의 각.

구면좌표계의 경우는 좌표값에 따라 한 점을 여러 좌표가 가리키는 경우가 있으므로, 각 변수의 범위를 보통 아래와 같이 제한한다.

$r\geq 0$

$0\leq \theta \leq \pi$

$0\leq \phi \leq 2\pi$

2. 직교 좌표계

직교 좌표계(直交座標系, 영어: rectangular coordinate system), 혹은 좌표평면은 임의의 차원의 유클리드 공간 (혹은 좀 더 일반적으로 내적공간)을 나타내는 좌표계의 하나이다. 이를 발명한 프랑스의 수학자 데카르트의 이름을 따 데카르트 좌표계(Cartesian coordinate system)라고도 부른다. 직교 좌표계는 극좌표계 등 다른 좌표계와 달리, 임의의 차원으로 쉽게 일반화할 수 있다. 직교 좌표계는 나타내는 대상이 평행이동(translation)에 대한 대칭을 가질 때 유용하나, 회전 대칭 등 다른 꼴의 대칭은 쉽게 나타내지 못한다. 일반적으로, 주어진 유클리드 공간에기저와 원점이 주어지면, 이를 이용하여 직교 좌표계를 정의할 수 있다.

가장 흔한 2차원 혹은 3차원의 경우, 직교 좌표를 통상적으로 라틴 문자 x, y, z로 적는다. 4차원인 경우, w나 (물리학에서 시공을 다루는 경우) t를 쓴다. 임의의 차원의 경우에는 첨자로 x_n의 꼴로 쓴다.

3. 좌표 변환

다른 3차원 좌표계로 변환하는 공식은 다음과 같다.

직교좌표계

직교좌표계에서 구면좌표계로 변환시:

$\begin{align} r &= \sqrt{x^2 + y^2 + z^2} \\ \theta &= \arccos\frac{z}{r} \\ \phi &= \arctan\frac{y}{x} \end{align}$

구면좌표계에서 직교좌표계로 변환시:

$\begin{align} x &= r \sin\theta \cos\phi \\ y &= r \sin\theta \sin\phi \\ z &= r \cos\theta \end{align}$

지리좌표계

${\delta}=90^\circ - \theta$ , or

${\theta}=90^\circ - \delta$ ,

원통좌표계

원통좌표계에서 구면좌표계로 변환시:

$r=\sqrt{\rho^2+z^2}$

${\theta}=\operatorname{arctan}(\rho,z)$

${\varphi}=\varphi \quad$

구면좌표계에서 원통좌표계로 변환시:

$\rho = r \sin \theta \,$

$\varphi = \varphi \,$

$z = r \cos \theta \,$

단위벡터

각 단위벡터의 직교좌표에서의 표현은 다음과 같다.

$\hat{\mathbf{r}} = \frac{\frac{d\mathbf{r}}{dr}}{\left|\frac{d\mathbf{r}}{dr}\right|} = \begin{bmatrix} \sin \theta \cos \phi \\ \sin \theta \sin \phi \\ \cos \theta \end{bmatrix}$

$\hat{\mathbf{\theta}} = \frac{\frac{d\mathbf{r}}{d\theta}}{\left|\frac{d\mathbf{r}}{d\theta}\right|} = \begin{bmatrix} \cos \theta \cos \phi \\ \cos \theta \sin \phi \\ -\sin \theta \end{bmatrix}$

$\hat{\mathbf{\phi}} = \frac{\frac{d\mathbf{r}}{d\phi}}{\left|\frac{d\mathbf{r}}{d\phi}\right|} = \begin{bmatrix} -\sin\phi \\ \cos\phi \\ 0 \end{bmatrix}$

- 참조 : 위키피디아 -

'Computer Graphics' 카테고리의 다른 글

회전행렬 Image Rotation matrix (0)	2014.07.23
COS값 SIN값 코사인값 싸인값 (0)	2014.03.13
프레임 버퍼 FBO(프레임 버퍼 오브젝트)란 frame buffer object (1)	2014.02.22
VBO(Vertex Buffer Object) 버텍스 버퍼 오브젝트란 (0)	2014.02.18
지오데식 돔이란(geodesic dome) 지오데식 돔 2V (2)	2014.02.11

현재글구면 좌표계(spherical coordinate system) 직교 좌표계(rectangular coordinate system)

#1인미디어 #크리에이터 #뉴미디어 #문화예술경영 #콘텐츠산업 #영상 #컴퓨터그래픽스 #컴퓨터비전

Today :
Yesterday :

익플루언서 :: ikfluencer

구면 좌표계(spherical coordinate system) 직교 좌표계(rectangular coordinate system)